13241 문제 링크
https://www.acmicpc.net/problem/1324
문제 설명
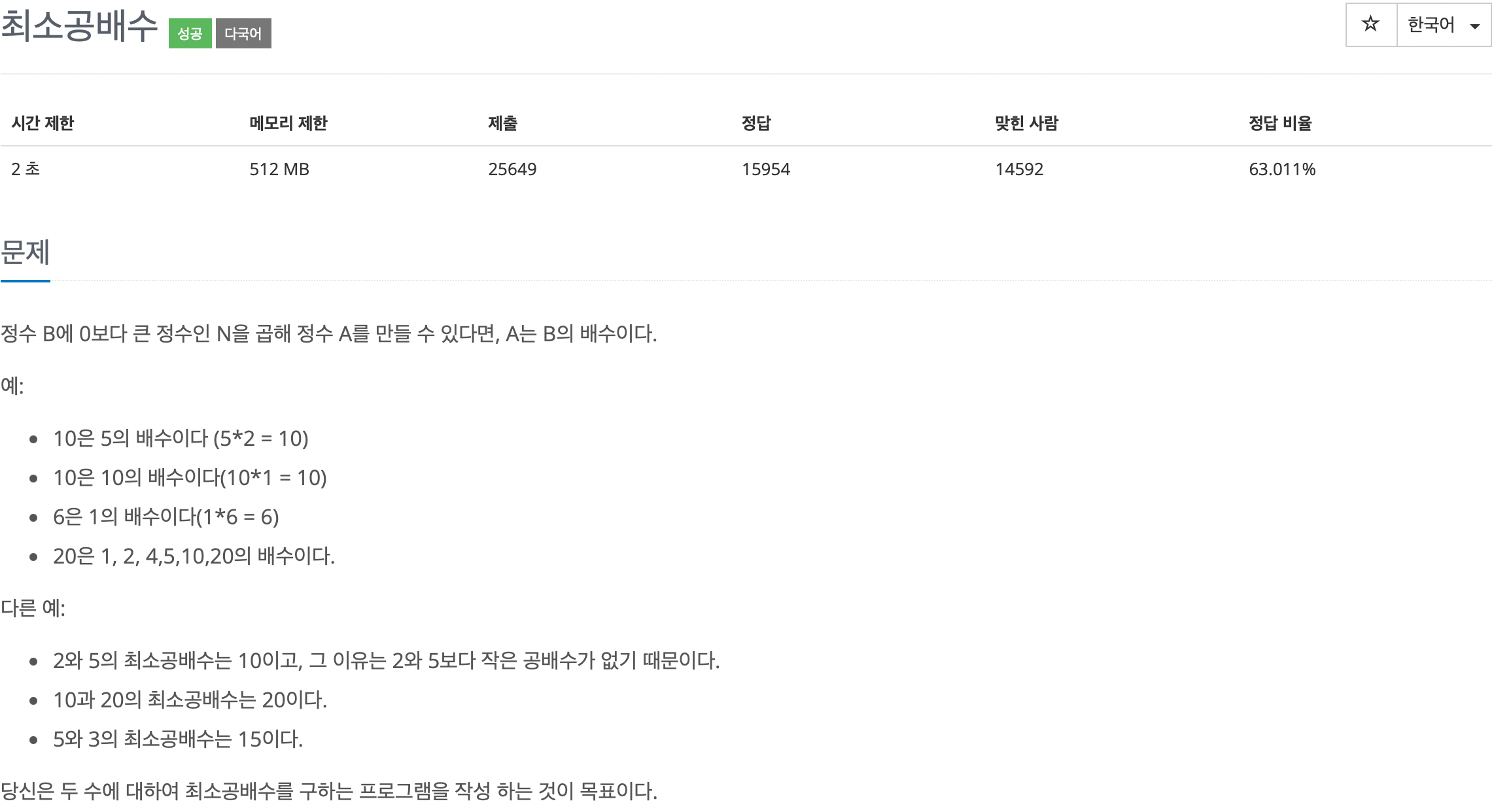
입출력
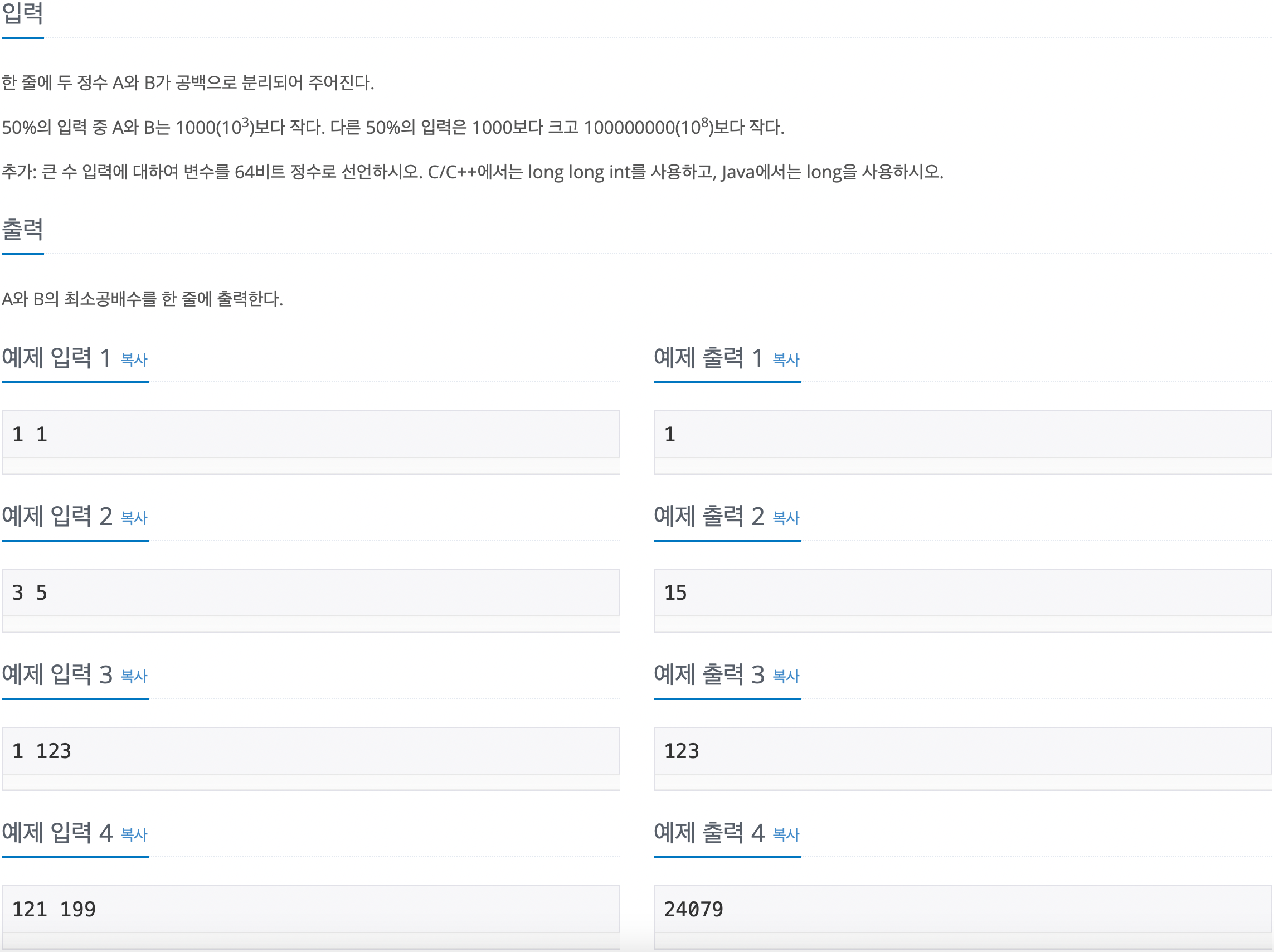
코드
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
|
import java.io.*;
import java.util.*;
public class Main {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
StringTokenizer input = new StringTokenizer(br.readLine());
long a = Long.parseLong(input.nextToken());
long b = Long.parseLong(input.nextToken());
long gcd = 0L;
long multi = a * b;
while(b != 0){
long temp = a % b;
a = b;
b = temp;
gcd = a;
}
long lcm = multi / gcd;
bw.write(String.valueOf(lcm));
bw.flush();
}
}
|
cs |
알고리즘 설명
해당 문제는 유클리드 호제법의 개념에 대해 알고있다면 전혀 어렵지 않은 문제였다고 생각합니다.
유클리드 호제법은 최대공약수를 효율적으로 구하는 알고리즘입니다.
유클리드 호제법은 두 수의 최대공약수(GCD)를 효율적으로 구하는 알고리즘입니다. 두 수 a 와 b 에 대해, a 를 b 로 나눈 나머지를 구하고, 그 나머지와 b 의 최대공약수를 반복적으로 계산하여 나머지가 0이 될 때까지 계속해서 진행되며, 가장 작은 수에서 최대공약수를 찾는 방식입니다.
최소공배수 또한 유클리드 호제법을 통해 얻은 최대공약수를 활용하여 구할 수 있습니다. 간단한 식은 이렇습니다.
$$ \text{LCM}(A, B) = \frac{A \times B}{\text{GCD}(A, B)} $$
코드 해석
유클리드 호제법으로 두 수의 GCD를 구하고, LCM(최소공배수)를 구하는 공식을 적용
'알고리즘 > 백준' 카테고리의 다른 글
| 백준 2346 풍선 터뜨리기 - JAVA (0) | 2025.01.27 |
|---|---|
| 백준 9184 신나는 함수 실행 - JAVA (0) | 2025.01.24 |
| 백준 28278 스택 2 - JAVA (0) | 2025.01.23 |
| 백준 17103 골드바흐 파티션 - JAVA (2) | 2025.01.22 |
| 백준 1929 소수 구하기 - JAVA (1) | 2025.01.21 |
