1929 문제 링크
https://www.acmicpc.net/problem/1929
문제 설명
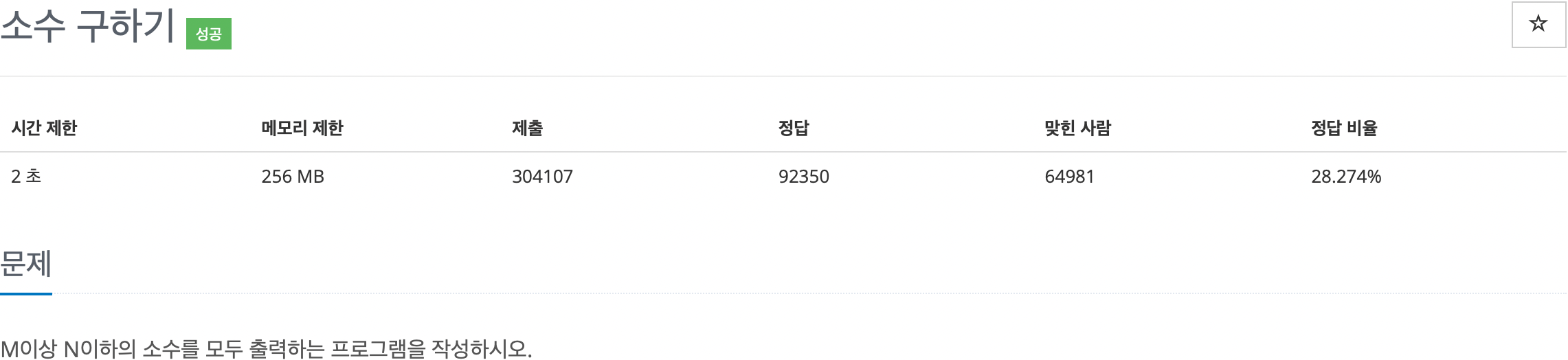
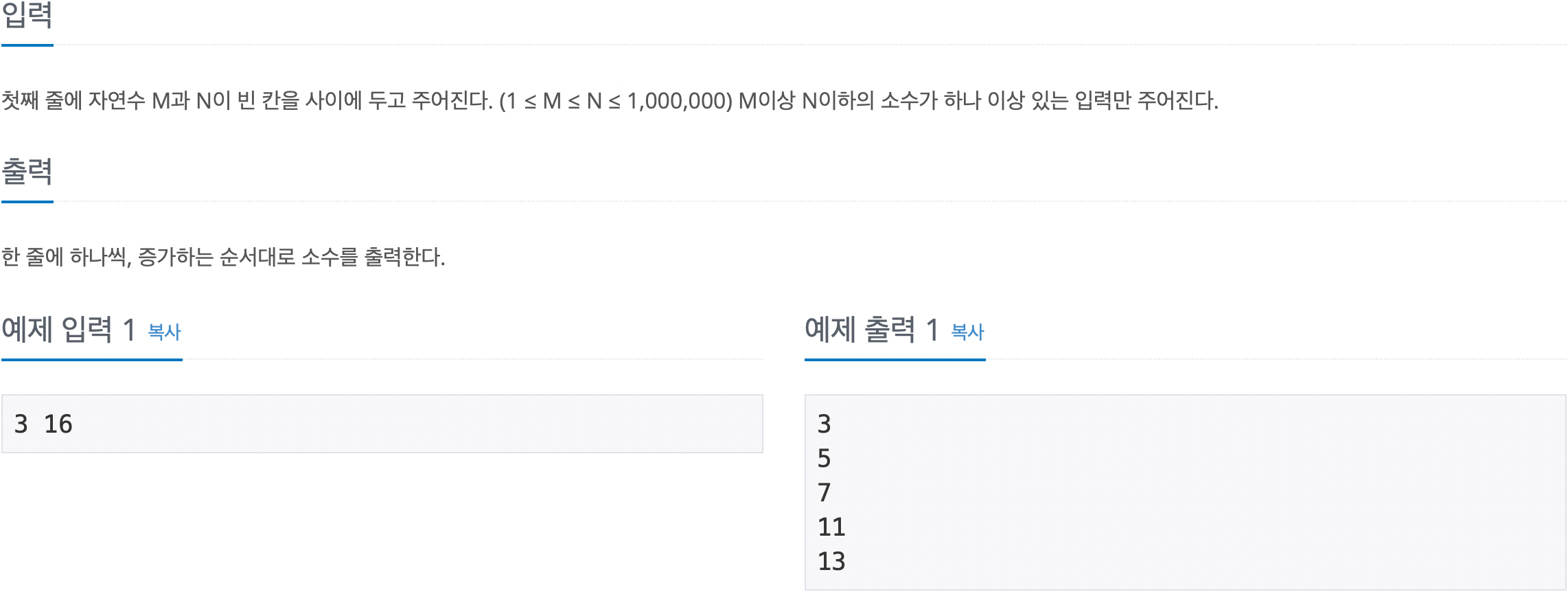
입출력
코드
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
|
import java.io.*;
import java.util.*;
public class Main {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
StringTokenizer st = new StringTokenizer(br.readLine());
int min = Integer.parseInt(st.nextToken());
int max = Integer.parseInt(st.nextToken());
boolean[] isPrime = new boolean[max + 1];
Arrays.fill(isPrime, true);
isPrime[0] = isPrime[1] = false;
for(int i = 2; i * i <= max; i++) {
if(isPrime[i]) {
for(int j = i * i; j <= max; j += i) {
isPrime[j] = false;
}
}
}
for(int i = min; i <= max; i++) {
if(isPrime[i]) {
bw.write(String.valueOf(i) + "\n");
}
}
bw.flush();
}
}
|
cs |
알고리즘 설명
해당 문제는 M값 부터 N값까지의 소수를 판별하여 모두 출력하는 문제입니다.
수의 범위가 1,000,000으로 최대값 자체는 크지 않아 일반적인 반복문으로 모든 수를 확인하는 방법도 가능하지만,
에라토스테네스의 체를 이용한 방식으로 접근하는 것이 다른 소수 판별 문제에서도 적용가능하다고 생각합니다.
에라토스테네스의 체는 주어진 범위 내에서 소수를 효율적으로 검색할 수 있습니다.
2부터 범위 내의 숫자(N) 까지 모두 나열하고, 2부터 마지막 숫자의 루트값(√N)안에 존재하는 소수의 배수를 차례대로 모두 지우는 방식입니다.
해당 과정을 이미지로 보여드리겠습니다.
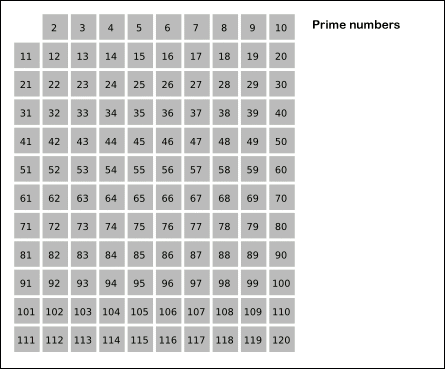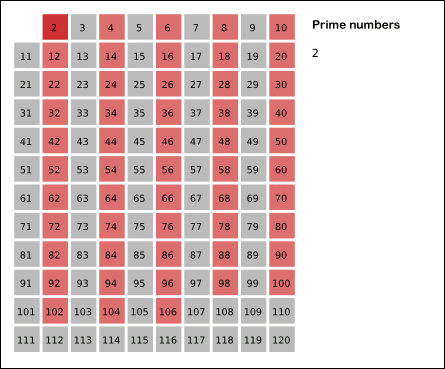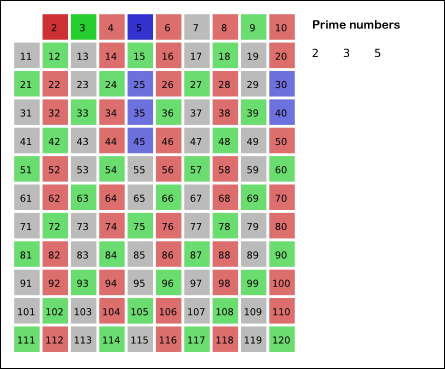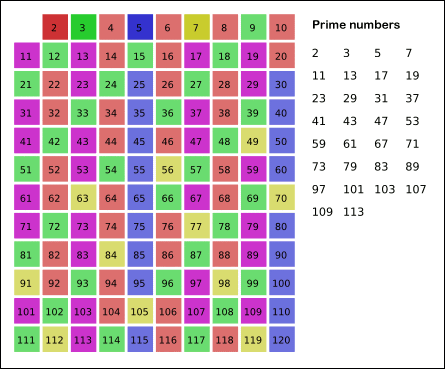
[ 출처 - 위키백과 : https://ko.wikipedia.org/wiki/에라토스테네스의_체- ]
해당 풀이 과정은 실제 시간복잡도 면에서도 유리합니다.
해당 알고리즘을 제외한 소수 판별법은 3가지 정도가 존재합니다.
표로 보여드리겠습니다.
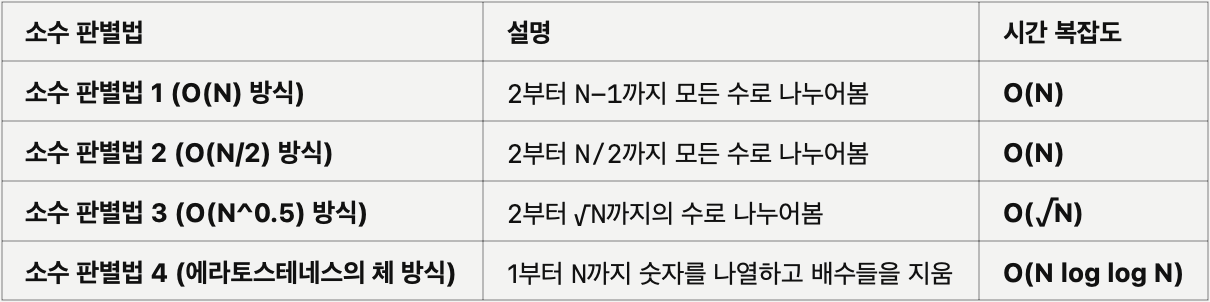
코드 해석
1. 크기가 max + 1인 isPrime 불리언 배열을 생성하고, 모든 값을 true로 설정
2. i는 2부터 i * i의 값이 max를 초과하지 않을때까지, i를 제외한 i 의 모든 배수를 false처리
2-1. 외부 루프에 의해 2부터 i*i <= max를 만족하는 수(=√N) 즉, 해당 범위 내의 소수(isPrime[i] == true인 경우)만 내부 루프 진행
ex) i = 4인 경우 i = 2일때 이미 소수가 아님(false)으로 처리되어 내부 루프를 돌지 않습니다.
2-2. 내부 루프에 의해 i * i 부터 max까지 isPrime[j] == false 처리
추가설명) i * i인 이유는 i * i보다 작은 수의 경우는 앞선 루프에서 모두 처리되었기 때문입니다.
3. 반복문을 통해 min부터 max까지 true인 값을 출력
'알고리즘 > 백준' 카테고리의 다른 글
| 백준 2346 풍선 터뜨리기 - JAVA (0) | 2025.01.27 |
|---|---|
| 백준 9184 신나는 함수 실행 - JAVA (0) | 2025.01.24 |
| 백준 28278 스택 2 - JAVA (0) | 2025.01.23 |
| 백준 17103 골드바흐 파티션 - JAVA (2) | 2025.01.22 |
| 백준 13241 최소공배수 - JAVA (0) | 2025.01.20 |
