17103 문제 링크
https://www.acmicpc.net/problem/17103
문제 설명

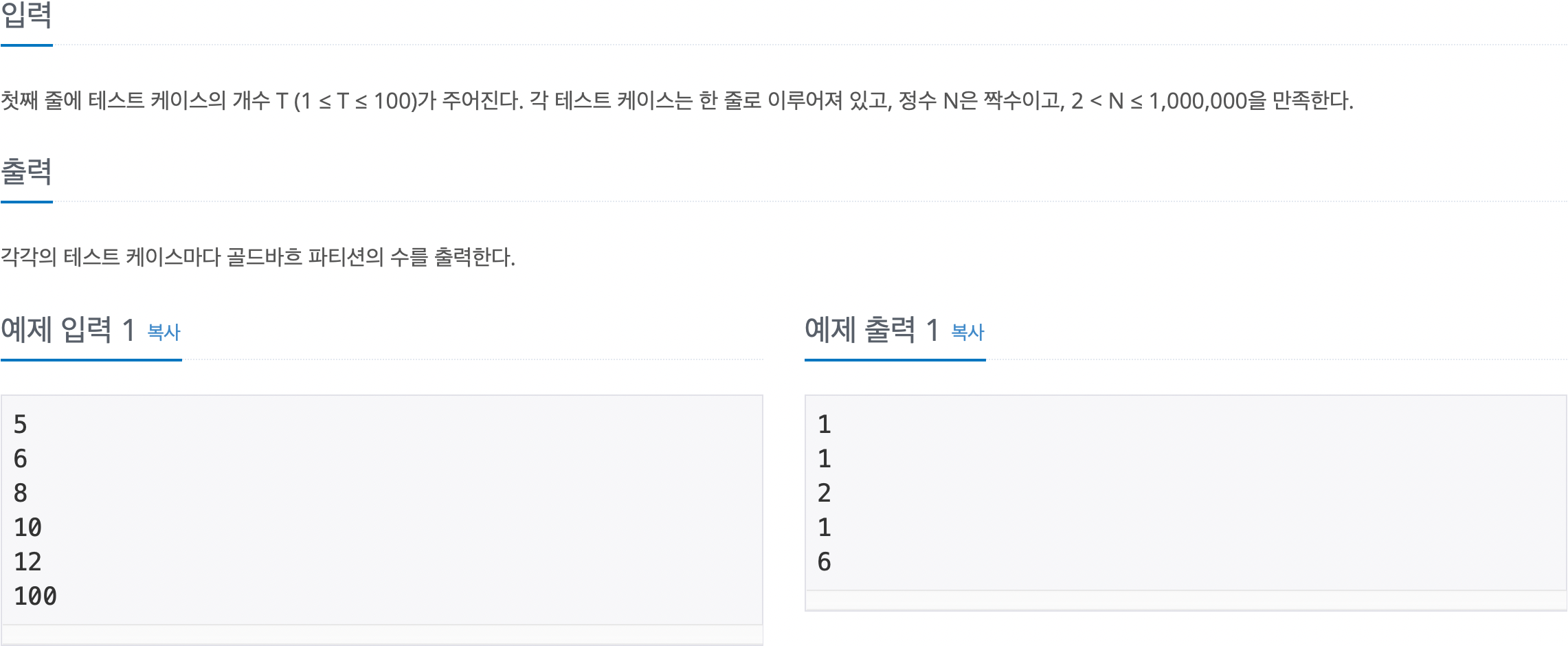
입출력
코드
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
|
import java.io.*;
import java.util.*;
public class Main {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
int input = Integer.parseInt(br.readLine());
List<Integer> nums = new ArrayList<>();
int maxNum = 0;
for(int i = 0; i < input; i++) {
int num = Integer.parseInt(br.readLine());
nums.add(num);
if(num > maxNum) maxNum = num;
}
boolean[] isPrime = new boolean[maxNum + 1];
Arrays.fill(isPrime, true);
for(int i = 2; i*i <= maxNum; i++) {
if(isPrime[i]) {
for(int j = i*i; j <= maxNum; j += i) {
isPrime[j] = false;
}
}
}
List<Integer> primes = new ArrayList<>();
for(int i = 2; i < maxNum; i++) {
if(isPrime[i]) primes.add(i);
}
for (int num : nums) {
int count = 0;
for(int j = 0; primes.get(j) <= num / 2; j++) {
int p1 = primes.get(j);
int p2 = num - p1;
if(isPrime[p2]) count++;
}
bw.write(String.valueOf(count) + "\n");
}
bw.flush();
}
}
|
cs |
알고리즘 설명
문제에 대한 풀이는 많을 것 같지만, 어떠한 풀이가 가장 효율적인지 생각해보는 것이 핵심인것 같습니다.
주어진 숫자 범위 내의 소수값을 찾고, 범위 내의 소수 중에서 중복을 포함한 소수 두 개를 더하여 주어진 숫자를 완성할 수 있는
즉, 골드바흐 파티션이 되는 수를 찾는 것입니다.
[ 골드바흐 파티션의 개수 세기 ]
p1 <= p2 조건이 만족되는 소수 p1과 소수 p2를 더했을 때, num 되려면, p1의 값은 반드시 num 절반값의 이하여야합니다.
두 소수의 순서만 다른 것은 같은 파티션이 라고 문제에 명시되어있으니, p1의 값만 찾아 카운팅하면 중복되는 쌍없이 파티션의 개수를 찾을 수 있습니다.
코드 해석
해당 문제는 연산을 중복되지 않게 푸는 것이 중요합니다.
입력한 숫자마다 해당 수 범위의 소수를 구하고, 불리언 배열을 생성하고, true/false값을 적용해주고, 골드바흐 파티션의 개수를 구하니까 5-6배 정도의 실행시간 차이를 보여줬습니다.

문제를 잘읽어보고 중복이 최소화 되는 풀이를 천천히 생각해본다면 그리 어렵지않은 문제라고 생각합니다.
입력한 숫자들을 nums라는 리스트에 담아줍니다.
그 중에서 가장 큰 수를 구하여 isPrime 불리언 배열을 생성하고, 에라토스테네스의 체 방식으로 소수를 판별합니다.
판별된 소수들을 다시 nums의 담긴 숫자들을 기준으로 골드바흐 파티션을 세는 알고리즘을 적용하면 됩니다.
'알고리즘 > 백준' 카테고리의 다른 글
| 백준 2346 풍선 터뜨리기 - JAVA (0) | 2025.01.27 |
|---|---|
| 백준 9184 신나는 함수 실행 - JAVA (0) | 2025.01.24 |
| 백준 28278 스택 2 - JAVA (0) | 2025.01.23 |
| 백준 1929 소수 구하기 - JAVA (1) | 2025.01.21 |
| 백준 13241 최소공배수 - JAVA (0) | 2025.01.20 |
